smadi 9 mars 2019
On trouve de nombreuses pages sur le web qui traitent des splines cubiques mais presque pas d'interpolations quadratiques. Le but de cet article est de combler cette lacune.

Soit une suite de cinq termes $u_0=1, u_1=3, u_2=4, u_3=1, u_4=2$.
On voudrait en donner une représentation graphique dans le plan.
La première solution est une représentation en escalier (Fig 1)
La deuxième est une représentation affine par morceaux (Fig 2)
Une autre solution consiste à représenter cette suite par une courbe lisse. (Fig 3)
Remarque
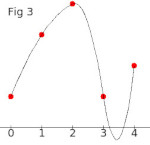
Les calculs exposés ci-dessous conduisent à la fonction quadratique par morceaux suivante
$\forall x \in [0,1[,\quad f(x)=1+2.5x-0.5x^2$
$\forall x \in [1,2[,\quad f(x)=3 +1.5(x-1) -0.5\left(x-1\right)^2$
$\forall x \in [2,3[,\quad f(x)=4 +0.5(x-2) -3.5\left(x-2\right)^2$
$\forall x \in [3,4],\quad f(x)=1 -6.5(x-3) +7.5\left(x-3\right)^2$
Sur $[0, 1[ et [1, 2[$ c'est la même.
Étant donné une suite finie $u_0, u_1, u_2,~...~,u_n$, on voudrait représenter cette suite dans le plan par une courbe passant par les points $(0,u_0),~(1,u_1),~ ... ~, (n,u_n)$ qui soit relativement «lisse». Par lisse on entend qu'il n'y ait ni saut ni brisure.
Nous allons construire ici une fonction définie par morceaux sur les intervalles $[0,1[, [1,2[, ... , [n-1, n]$, par des plynômes du second degré.
$P_0(X)=u_0+a_1 X+b_0 X^2$ sur $[0, 1[$,
$P_1(X)=u_1+a_1(X-1)+b_1\left(X-1\right)^2$ sur $[1,2[$
et ainsi de suite jusqu'à
$P_{n-1}(X)=u_{n-1}+a_{n-1}(X-n+1)+b_{n-1}\left(X-n+1\right)^2$ sur $[n-1, n]$.
Nous sommes déjà assurés qu'elle passe par les points voulus, sauf le dernier : $\forall k=0, 1, ... , n-1 \quad P_k(k)=u_k$
Nous ajoutons alors $P_{n-1}(n)=u_n$
Il faudrait de plus qu'aux points charnières les pentes soient les mêmes, c'est à dire $\forall k=1,2, ... , n-1 \quad P\prime_{k-1}(k)=P\prime_{k}(k)$
$\forall k=0, 1, ... ,n-1$ notre fonction est définie sur $[k, k+1[$ par le polynôme $P_k$ :
$\forall X\in [k, k+1[, \quad P_k(X)=u_k+a_k(X-k)+b_k\left(X-k\right)^2$
donc $\forall X\in [k, k+1[, \quad P_k\prime(X)=a_k + 2b_k(X-k)$
Aux extrémités on aura: $P_0(0)=u_0$ et $P_{k-1}(n)=u_n$.
Puis pour chaque point d'indice $k=1,~...,~n-1$
$P_{k-1}(k)=u_k=P_k(k)$ et $P\prime_{k-1}(k)=P\prime_k(k)$
On obtient les formules de récurrence, pour tout $k=1$, ..., $n-1$
$a_k=a_{k-1}+2b_{k-1}$ et $a_{k-1}+b_{k-1}=u_k-u_{k-1}$.
soit :
$a_k=2(u_k-u_{k-1})-a_{k-1}$ et $b_{k-1}=u_k-u_{k-1}-a_{k-1}$.
Tandis que $P_{n-1}(n)=u_n$ fournit le dernier $b_k$ :
$b_{n-1}=u_n-u_{n-1}-a_{n-1}$
On peut alors calculer les $a_k$ et $b_k$ en se donnant une valeur arbitraire à $a_0$ (qui est en quelque sorte l'angle de tir au départ puisque $P\prime_0(0)=a_0$). Alors $b_0=u_1-u_0-a_0$, puis de proche en proche on obtiendra $a_1$, $b_1$, $a_2$, $b_2$, etc.
Une manière de choisir cet angle de tir serait de considérer le polynome d'interpollation de Lagrange construit à partir de quelques uns des premiers points. Par exemple avec les trois premiers points, le polynome d'interpolation de Lagrange s'écrit
$$L(X)=u_0\dfrac{(X-1)(X-2)}{(0-1)(0-2)}+u_1\dfrac{X(X-2)}{(1-0)(1-2)}+u_2\dfrac{X(X-1)}{(2-0)(2-1)}$$
et après simplification on obtient :
$$L(X)=\dfrac{1}{2}(u_0-2u_1+u_2)X^2+\dfrac{1}{2}(-3u_0+4u_1-u_2)X+u_0$$
d'où : $L\prime(0)=\dfrac{1}{2}(-3u_0+4u_1-u_2)$ qui est notre $a_0$
Remarque 1 On pourrait (cf. Calcul de $a_0$ dans le cas d'une suite de points) tout aussi bien résoudre en $a$ et $b$ les équations $y=u_0+ax+bx^2$ pour que la parabole passe par les points $(1, u_1)$, $(2,u_2)$.
Remarque 2 Avec sympy (voir Sympy ou Sympy solver)
>>> from sympy import *>>> var('a b u0 u1 u2 x')(a, b, u0, u1, u2, x)>>> linsolve([u0+a+b-systemdu1, u0+2*a+4*b-u2], (a,b)){(-3*u0/2 + 2*u1 - u2/2, u0/2 - u1 + u2/2)}
Étant donné une suite finie de $n+1$ termes :
$u_0, u_1, u_2,~...~,u_n$,
On choisit $a_0$, $a_0=-\dfrac{3}{2}u_0+2u_1-\dfrac{1}{2}u_2$ serait un bon choix.
On calcule les coefficients $a_k$ et $b_k$ par :
pour $k=1, ... ,n-1 \quad a_k=2(u_k-u_{k-1})-a_{k-1}$
et pour $k=0, ... ,n-1 \quad b_k=u_{k+1}-u_k-a_k$.
alors la fonction définie par morceaux sur $[0,n]$ par
$\forall k=0,1,...,n-1\quad \forall x \in [k,k+1[\quad f(x)=u_k+a_k(x-k)+b_k\left(x-k\right)^2$ et $f(n)=u_n$.
est une spline quadratique de la suite $u_k$.
Considérons maintenant $n+1$ points $(x_0, y_0),~(x_1, y_1),~...~,~(x_n,y_n)$ où $\forall k=0,1, ... , n-1,\quad x_k\lt x_{k+1}$ et la fonction $f$ définie sur $[x_0,x_n]$ par :
$\forall k=0,1, ... , n-1, \forall x\in [x_k,x_{k+1}[ \quad f(x)=y_0+a_k(x-x_k)+b_k\left(x-x_k\right)^2$
et $f(x_n)=y_n$.
Cherchons l'équation de la parabole passant par les trois premiers points.
Soit $g(x)=y_0+a(x-x_0)+b\left(x-x_0)\right)^2$.
Nous ne sommes intéressés que par $g'(x_0)=a$
$g(x_1)=y_1$ donc $y_0+a(x_1-x_0)+b\left(x_1-x_0)\right)^2=y_1$
$g(x_2)=y_2$ donc y_0+a(x_2-x_0)+b\left(x_2-x_0)\right)^2=y_2$
On obtient les système où les inconnues sont $a$ et $b$
$ \left\{ \begin{array}{c} (x_1-x_0)a+\left(x_1-x_0\right)^2 b=y_1-y_0 \\ (x_2-x_0)a+\left(x_2-x_0\right)^2 b=y_2-y_0 \end{array}$
On calcule $a$ (par la méthode des déterminants)
$a=\dfrac{\left(x_2-x_0\right)^2(y_1-y_0)-\left(x_1-x_0\right)^2(y_2-y_0)}{(x_1-x_0)\left(x_2-x_0\right)^2-(x_2-x_0)\left(x_1-x_0\right)^2}$
Ou si on veut :
$a=\dfrac{-(x_1+x_2-2x_0)(x_2-x_1)y_0+\left(x_2-x_0\right)^2y_1-\left(x_1-x_0\right)^2y_2}{(x_2-x_1)(x_2-x_0)(x_1-x_0)}$
qui est notre $a_0$ pour la suite.
Avec Sympy
>>> from sympy import *>>> var('x x0:3 y0:3 a b')(x, x0, x1, x2, y0, y1, y2, a, b)>>> s=linsolve([(x1 - x0)*a + b*(x1 - x0)**2 - y1 + y0, \... (x2 - x0)*a + b*(x2 - x0)**2 - y2 + y0], (a, b))>>> list(s)[0][0] # seule la valeur de a nous intéresse(-x0**2*y1 + x0**2*y2 + 2*x0*x1*y0 - 2*x0*x1*y2 - 2*x0*x2*y0+ 2*x0*x2*y1 - x1**2*y0 + x1**2*y2 + x2**2*y0 - x2**2*y1)/(x0**2*x1 - x0**2*x2 - x0*x1**2 + x0*x2**2 + x1**2*x2 - x1*x2**2)
en exploitant le printer latex de sympy
>>> latex(_)
on obtient (moyennant quelques ajustements) l'expression moins illisible :
$a_0=\dfrac{- x_{0}^{2} y_{1} + x_{0}^{2} y_{2} + 2 x_{0} x_{1} y_{0} - 2 x_{0} x_{1} y_{2} - 2 x_{0} x_{2} y_{0} + 2 x_{0} x_{2} y_{1} - x_{1}^{2} y_{0} + x_{1}^{2} y_{2} + x_{2}^{2} y_{0} - x_{2}^{2} y_{1}}{x_{0}^{2} x_{1} - x_{0}^{2} x_{2} - x_{0} x_{1}^{2} + x_{0} x_{2}^{2} + x_{1}^{2} x_{2} - x_{1} x_{2}^{2}}$
$
Pour être franc j'ai juste vérifié que mon calcul concorde avec la solution fournie par sympy en soustrayant le développement avec expand.
Soit $f$ la fonction affine par morceaux sur les $[a_k, a_{k+1}[$
$\forall k=0,1, ... , n-1 \quad \forall x\in[x_k,x_{k+1}[ \quad f(x)=y_k+a_k(x-x_k)+b_k\left(x-x_k\right)^2$
et $f(x_n)=y_n$.
Donc sur $[a_k, a_{k+1}[$ on a $f'(x)=a_k+2b_k(x-x_k)$
Le raccordement en $x_{k+1}$ donne :
$y_k+a_k(x_{k+1}-x_k)+b_k\left(x_{k+1}-x_k\right)^2=y_{k+1}$
Et la tangente commune en $x_{k+1}$ donne
$a_k+2b_k(x_{k+1}-x_k)=a_{k+1}$
D'où l'on tire nos formules de récurrence :
$a_{k+1}=2\dfrac{y_{k+1}-y_k}{x_{k+1}-x_k}-a_k$
$b_k=\dfrac{y_{k+1}-y_k-a_k(x_{k+1}-x_k)}{\left(x_{k+1}-x_k\right)^2}}$
Étant donné une suite de $n+1$ points $(x_0,y_0),(x_1,y1), ... ,(x_n,y_n)$
on calcule
$a_0=\dfrac{-(x_1+x_2-2x_0)(x_2-x_1)y_0+\left(x_2-x_0\right)^2y_1-\left(x_1-x_0\right)^2y_2}{(x_2-x_1)(x_2-x_0)(x_1-x_0)}$
puis on calcule les coefficients $a_k$ et $b_k$ comme suit :
pour $k=0,1, ... , n-2\quad a_{k+1}=2\dfrac{y_{k+1}-y_k}{x_{k+1}-x_k}-a_k$
et pour $k=0,1, ... , n-1\quad b_k=\dfrac{y_{k+1}-y_k-a_k(x_{k+1}-x_k)}{\left(x_{k+1}-x_k\right)^2}}$
alors la fonction définie par morceau sur $[x_0,x_n]$ par :
$\forall k=0,1,...,n-1\quad \forall x \in [k,k+1[\quad f(x)=y_k+a_k(x-x_k)+b_k\left(x-x_k\right)^2$
et pour $k=n$, $f(x_n)=y_n$
est une spline quadratique des points $(x_k,y_k)$
Un article de la société des profs de sciences de Neuchâtel(Suisse)
Polytech-Lille(Programmes en C)